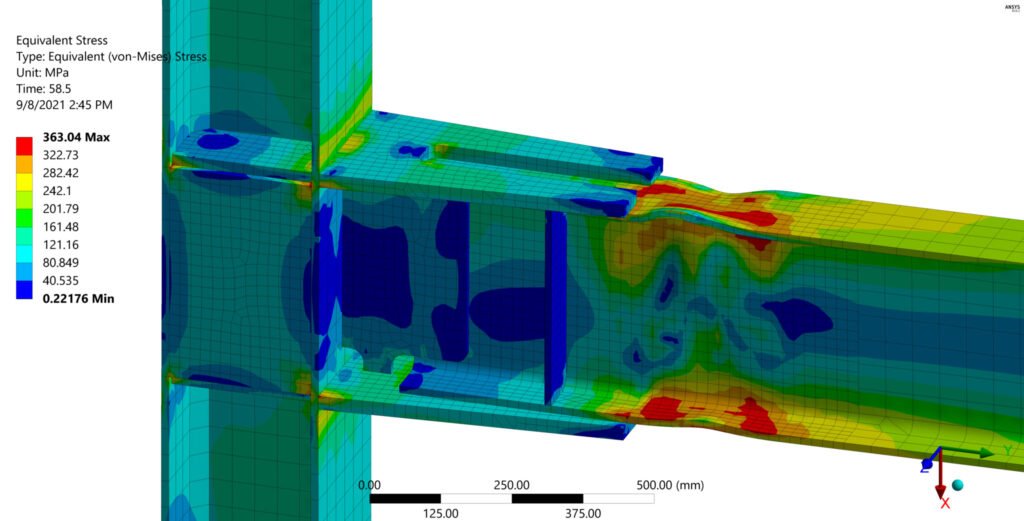
Análisis de pandeo por elementos finitos

Se define la carga de Euler como la máxima carga crítica que puede resistir una columna antes que se vuelva Inestable. Para Miembros robustos la falla puede ocurrir por fluencia a compresión en vez de pandeo. La carga bajo la cual ocurre el pandeo es función de su esbeltez tal como se ilustra en la siguiente expresión:

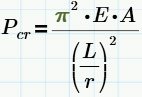
Donde E es el módulo de elasticidad del material, I es el Momento de Inercia del área transversal con respecto al eje principal menor y L es la longitud del miembro entre puntos de soporte. Para que la anterior ecuación sea válida, el miembro debe ser elástico y sus extremos deben estar restringidos a traslaciones pero no a Rotaciones (Condición Articulada). Esta Extraordinaria ecuación fue formulada por el matemático suizo Leonhard Euler quien la publico en 1957 denominada carga de pandeo de Euler.

Conociendo que el momento de Inercia es igual al área multiplicado por el radio de giro al cuadrado, se reescribe la anterior ecuación somo sigue:

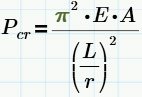
Sí la carga crítica se divide entre el área de la sección transversal, se obtiene el esfuerzo crítico de pandeo (Ecuación E.3-4 AISC 360-10):

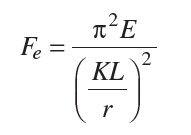
El pandeo se presentará tan pronto como la carga alcance el valor critico de Euler y la columna se volverá inestable respecto al eje principal correspondiente a la relación de esbeltez más grande, este eje es usualmente el de menor momento de Inercia. Para tener en cuenta el efecto de otros tipos de apoyos sobre la resistencia critica de pandeo se introduce un factor K, donde la siguiente tabla describe sus valores característicos.

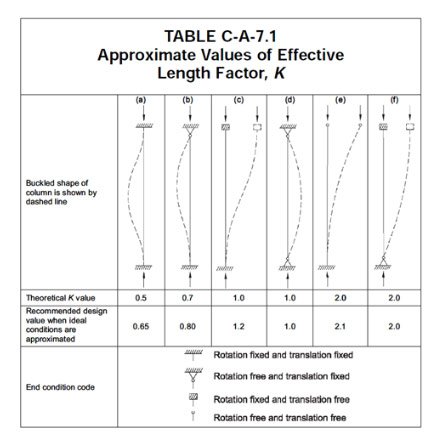
Por medio de un modelo de elementos finitos se puede encontrar los valores correspondientes con las cargas criticas de pandeo ó en caso de tener incertidumbre sobre el factor k, se puede precisar bajo el mismo análisis.

Como ejercicio de verificación se plantea el cálculo de la carga crítica de pandeo para una Columna de 750 cm de altura, Condición de apoyo tipo Cantilever, Conformada con un Perfil de acero doble T Europeo de referencia IPE-360 Acero A-36.

Las características geométricas del perfil son área=72.70cm2, radio de giro de menor Inercia=3.788cm, Módulo de elasticidad del acero 29000 ksi. Factor k=2.0 de acuerdo con los valores de la tabla C-A-7.1. Reemplazando estos valores en la Ecuación de Euler La carga crítica de pandeo es de 9328 kgf.

Para el modelo Numérico se implementaron elementos tipo Shell con espesores y aceros Indicados anteriormente para este perfil. Se aplico una carga unitaria sobre los 7 nodos superiores del perfil, para un total de 7 kg. Al correr un análisis de pandeo en el software Sap2000 el programa nos reporta el factor de escala de carga total introducida conforme a cada modo de pandeo.

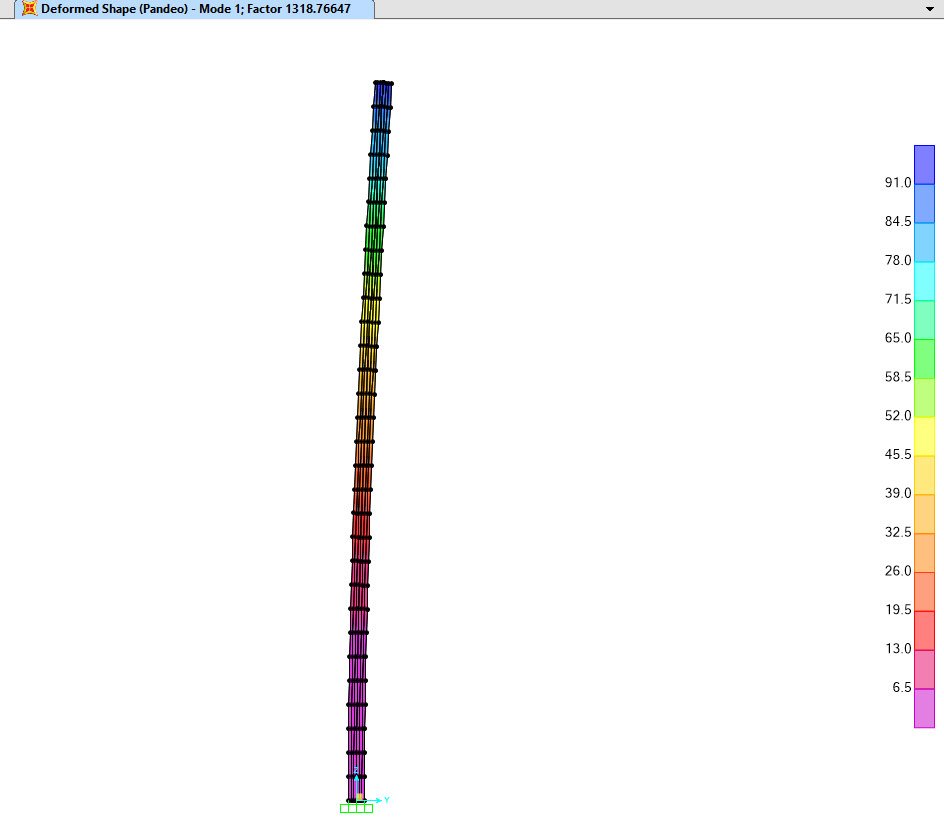
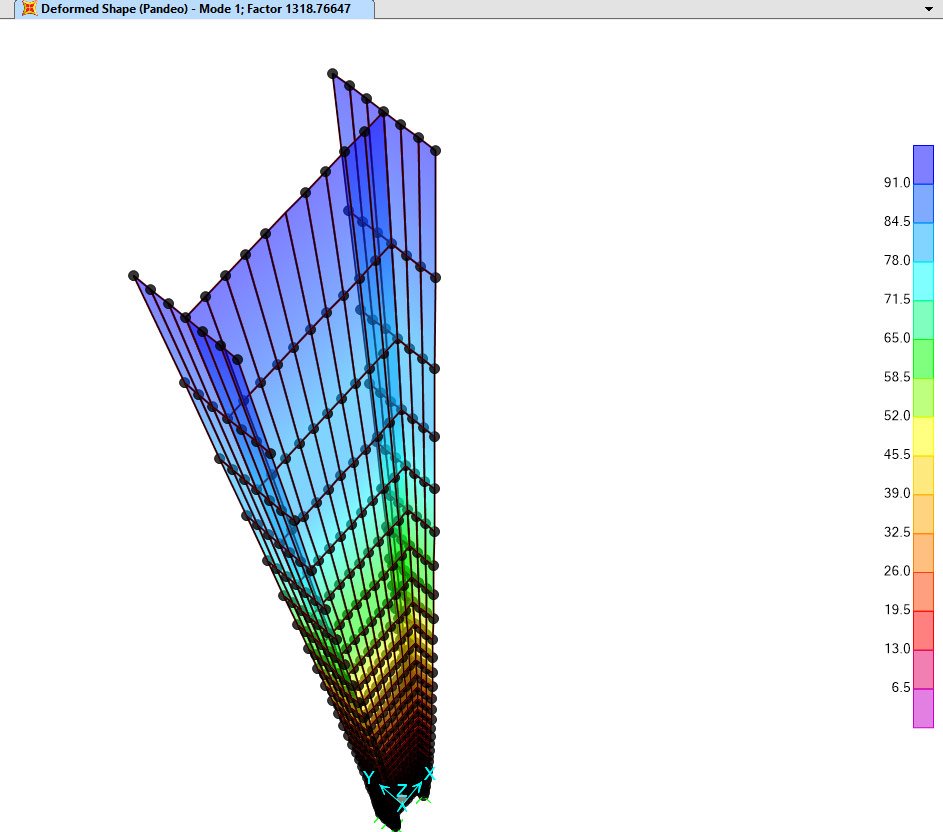
Modo 1 de pandeo. Factor de Escala 1318.766, Carga crítica de pandeo = 7kgf x 1318.766=9231kgf. El resultado bajo la ecuación de Euler es de 9328kgf, para un porcentaje de error de 1.03%

Adicionalmente puedo obtener los valores para los modos 2 y 3.

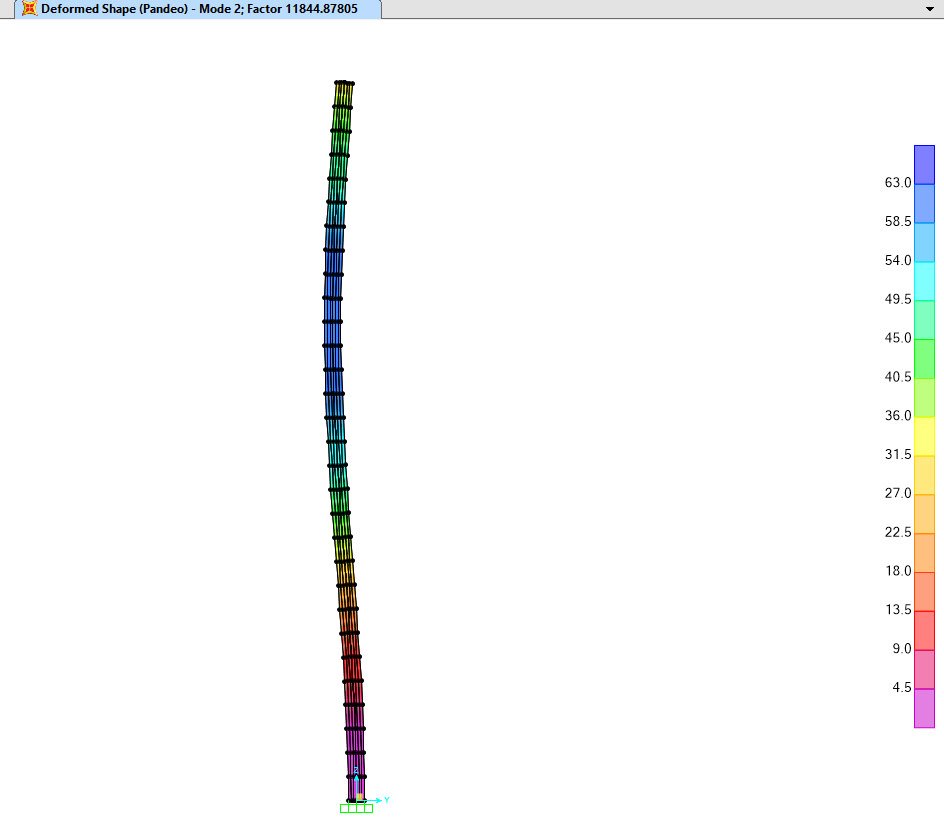
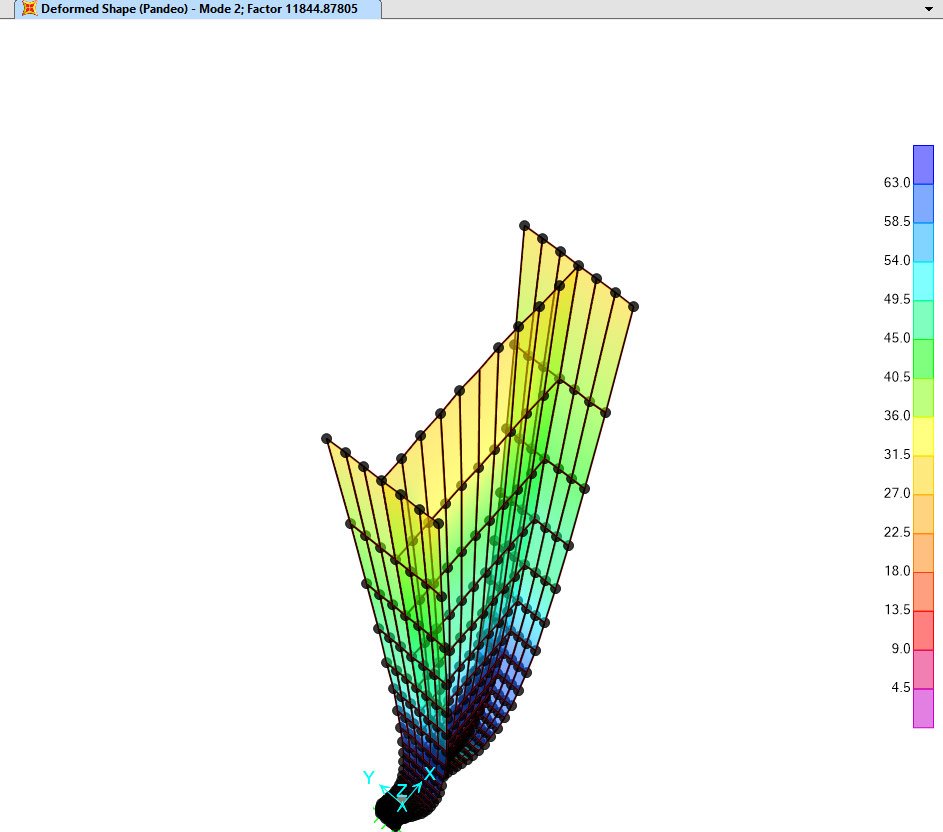
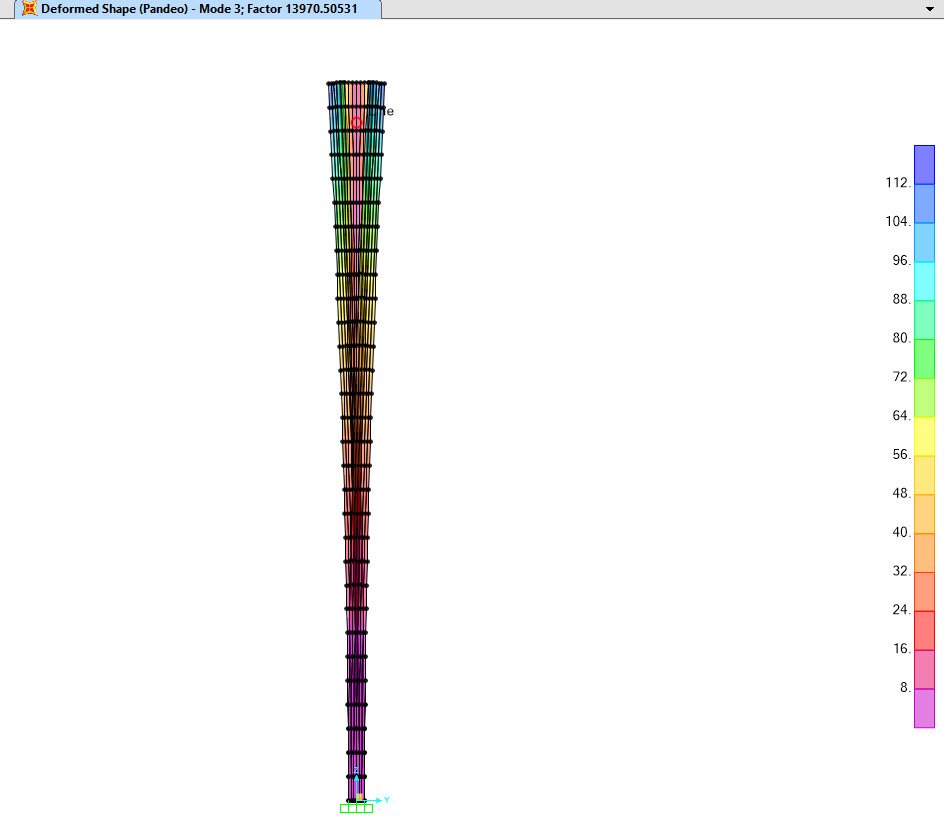
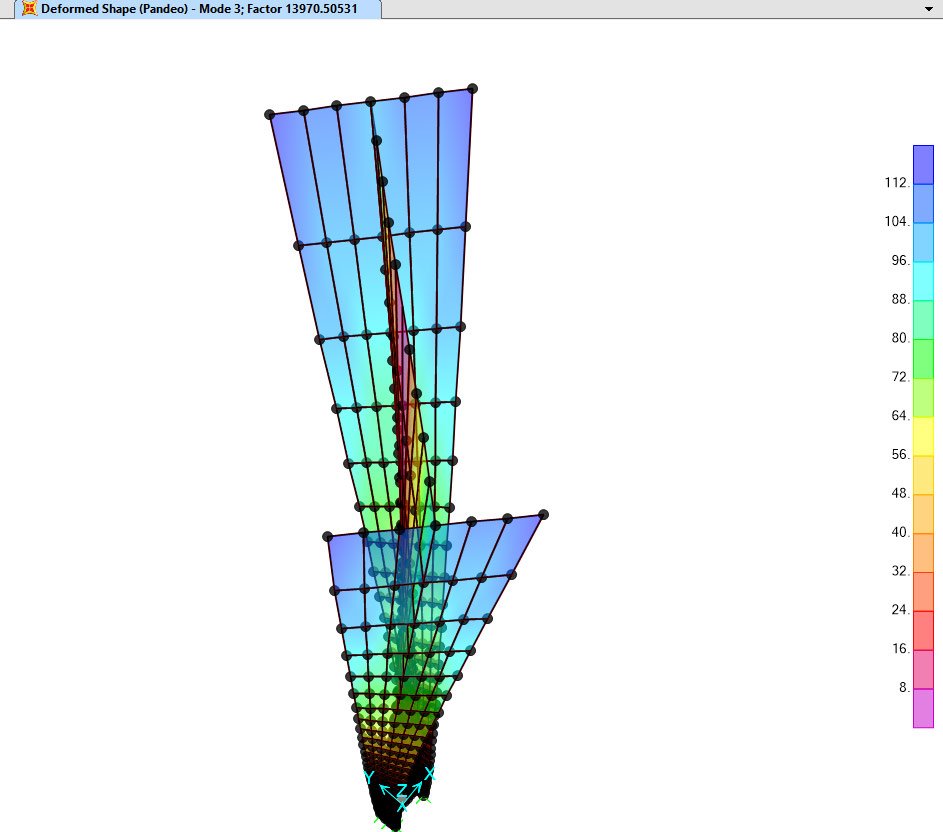
Para geometrías asimétricas, Los modelos por elementos finitos permiten predecir la respuesta estructural de manera sencilla, siempre y cuando el Ingeniero estructural cuente con la sensibilidad necesaria en el manejo de la herramienta e interpretación de resultados.

Planteamos un procedimiento detallado para la obtención de la curva de resistencia a compresión de un perfil IPE-360 A-36, de acuerdo con las recomendaciones de la AISC360-10. Visita Nuestro Toolshop.

https://goratools.com/product-page/resistencia-a-compresi%C3%B3n-perfil-ipe-360-astm-a-36